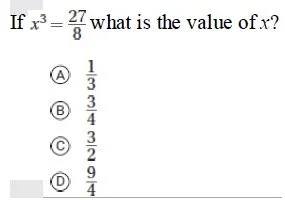Using Approximation and Test-Taking Techniques to Avoid Doing Math on the Math Sections of the ACT and SAT

Written by Josh, Massachusetts Institute of Technology

Standardized tests are designed to evaluate your ability to think, not your knowledge base. Thus, doing well on a standardized test is more dependent on good test-taking techniques than knowing the right answer to a question. In the math sections of the ACT and SAT, approximation, elimination, and identification of uniqueness are the most important skills you’ll be able to use to minimize silly errors, speed up your timing, and statistically optimize the probability of getting a correct answer. 

For instance, consider the following problem:

The first step here should be to eliminate choice A, since the numerator is 1 and 1 * 1 * 1 (13) is 1. Using the same logic, 93 is way bigger than 27. That leaves choices B and C. Since taking the cube root of a fraction requires taking the cube root of the numerator and denominator, we can recognize that we have a small denominator, so choice B is out. We do not need to know any more than that. Choice C is the correct answer.

A very important point here is that you should never solve a math problem all the way through to an answer. You should first eliminate all incorrect answer choices based on key superficial features of what you know the right answer should be. Then, you should only do enough math to convince yourself that the wrong answers are wrong, rather than trying to guess the right answer. Statistically, you’ll be right more of the time and you will avoid silly errors.

In addition, a good strategy is to use as little of your brain on memory and mental calculations as possible. The more of your thought processes you write down, the less of your brain will be occupied by unnecessary processing. Thus, more of your brain will be free to think through a problem and catch errors.

Other key factors of answer choices are the number of digits the right answer should have; whether an answer should be positive or negative, odd or even; and differences in the last digit between answer choices.

For example, consider the following problem:

 Obviously, the right approach here is to multiply 4,900 people per square mile by 139 square miles of land. The fastest way to do this is to eliminate answer choices based on superficial features, rather than calculating the product. Here, we know that 4,900 has four digits and 139 has three digits. A four-digit number times a three-digit number that is less than around 210 will have six digits. Thus, the right answer is C and we don’t even need to calculate anything.

This is the best set of strategies to use on the math section to give yourself as much time as possible, maximize correct answers, and minimize silly errors.